Вахчилка — удивительное место, которое нельзя не посетить любителю рыбной ловли. Это маленькое
Серый сурок (marmota baibacina kastsch) — один из видов сурков, распространенный на территории
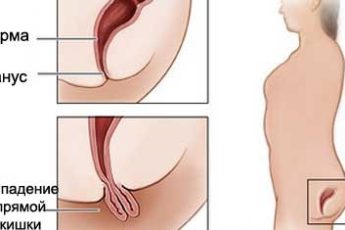
Выпадение прямой кишки или проктоз – это состояние, при котором прямая кишка выходит из анального отверстия.
Граб обыкновенный (Martes martes) – вид млекопитающих из семейства горностаевых. Эти млекопитающие отличаются
Ошейник Форесто – популярное средство для защиты собак от насекомых и паразитов. Этот уникальный ошейник
Блесна трубка является одним из наиболее эффективных и популярных видов рыболовных приманок.
Любительская рыбалка — это не только увлекательное времяпрепровождение, но и поистине уникальная возможность
Бобры — это удивительные создания, которые умеют самостоятельно строить гигантские деревянные плоты и дамбы.
В наше время пожары и взрывы на различных объектах стали не редкостью. К сожалению, такие происшествия
Рыбалка на усача – это увлекательное и захватывающее занятие, которое привлекает множество людей.
В мире винного искусства существует множество разных вин, каждое из которых имеет свой уникальный вкус и аромат.
Палешка — удивительное место, которое поразит всех любителей рыбалки. Сочетание красивых пейзажей
Зимняя рыбалка — это отличная возможность провести время на свежем воздухе и насладиться увлекательным хобби.
Любительский рыболов охочется почувствовать непередаваемую эйфорию от успешной рыбалки в самые неподходящие
Казан является одной из самых популярных посудин для приготовления различных блюд в нашей кухне.
Тоз-34 – это высококачественный и надежный продукт, который пришел на рынок с целью удовлетворить потребности
В 2023 году вступают в силу новые изменения в правилах охоты и рыбалки, которые предусматривают значительно
Лето — идеальное время для занятий рыболовством. Многие любители рыбалки предпочитают спиннинговую